HISTOGRAMAS
Básicamente el histograma es la representación gráfica de las frecuencias relativas con las que aparecen los distintos niveles de grises en una imagen determinada. En general se representa como un gráfico de barras, en el que las abscisas son los distintos niveles de grises de la imagen y las ordenadas la cantidad de veces con la que cada color aparece en la imagen. El histograma proporciona información sobre el brillo 6 y el contraste de la imagen, y puede ser utilizado para ajustar estos parámetros, eliminar ciertas tonalidades molestas, etc.

FILTRO ESPACIAL
El empleo de mascaras espaciales para el procesamiento de imágenes se denomina filtrado espacial. Entre los filtros espaciales lineales se encuentran los filtros pasa bajo, pasa alto, y pasa banda. Los denominados filtros pasa bajo atenúan o eliminan las componentes de alta frecuencia a la vez que dejan pasar las frecuencias bajas. Las componentes de alta frecuencia caracterizan los bordes y los restantes detalles muy marcados de la imagen, por ello el efecto de introducir un filtro de paso bajo es el de hacer mas borrosa la imagen. De forma similar, los filtros de paso alto atenúan o eliminan las componentes de baja frecuencia. Como estas componentes son las responsables de las características lentamente variables de la imagen, como el contraste global y la intensidad media, el resultado neto de un filtrado de paso alto es la reducción de estas características y, en correspondencia, una aparente agudización de los bordes y de los restantes detalles finos. Un tercer tipo de filtrado, denominado filtrado de paso banda, elimina unas regiones elegidas de frecuencia intermedias. Estos filtros se emplean para la restauración de imágenes.
Operador de Roberts
Es un operador no lineal simple de calcular, ya que sólo usa una ventana (también llamada filtro, plantilla, máscara, kernel) de tamaño 2x2


La magnitud del gradiente se calcula mediante la siguiente aproximación, puesto que Gx y Gy son aproximaciones de las derivadas parciales con respecto a x e y respectivamente.
Operador de Sobel
Este operador toma en cuenta todos los píxeles vecinos al píxel de interés. Este operador funciona aplicando una ventana de tamaño 3x3 sobre todos los píxeles de la imagen.

Con la constante c=2.
Estos operadores de gradiente pueden implementarse utilizando máscaras de convolución,
Es importante notar que este operador le da más peso a los píxeles más cercanos al centro de la máscara.
Operador de Prewitt
Operador laplaciano
Es el equivalente bidimensional de la segunda derivada [2], la fórmula para una función f(x,y)
Combinando las dos ecuaciones en un único operador, se puede usar la siguiente máscara para aproximar el laplaciano.
El algoritmo de Canny está considerado como uno de los mejores métodos de detección de contornos, mediante el empleo de máscaras de convolución, optimizando los tres criterios de detección, localización y respuesta única ante un borde.
El algoritmo consiste básicamente en cinco fases:
1. Suavizado de la imagen mediante una gaussiana para reducir los efectos del ruido.
2. Convolución de la imagen por operadores de gradiente direccionales.
3. Supresión de los gradientes que no son máximos en la dirección del contorno.
4. Aplicación de un umbral adaptativo con histérisis para distinguir los contornos reales del ruido. 5. Integración de los contornos detectados a diferentes escalas en un solo mapa de contornos consistentes.
2. Convolución de la imagen por operadores de gradiente direccionales.
3. Supresión de los gradientes que no son máximos en la dirección del contorno.
4. Aplicación de un umbral adaptativo con histérisis para distinguir los contornos reales del ruido. 5. Integración de los contornos detectados a diferentes escalas en un solo mapa de contornos consistentes.
Este operador es la combinación de un filtro gaussiano con una aproximación del gradiante , la cual es sensible al borde en la dirección del máximo cambio. El detector de bordes de Canny es la primera derivada de una gausiana.
UMBRALIZACIÓN
Se considera el histograma de niveles de gris correspondiente a una imagen compuesta de objetos oscuros sobre un fondo luminoso, de forma que los píxeles en los objetos y el fondo tienen niveles de grises agrupados en dos modas dominantes.
Una forma obvia de extraer los objetos del fondo es seleccionar un umbral T que separe estas modas. Es decir, obtener:

Esta ecuación puede tener muchas modificaciones. Una posible es segmentar la imagen en regiones de píxeles con nivel de gris en un conjunto D y el resto como fondo. También se puede utilizar umbrales múltiples, lo que produce imágenes no binarias con conjunto muy limitado de niveles de gris, el proceso sería:

Es claro que para hacer la segmentación más robusta, el umbral debería ser seleccionado automáticamente por el sistema. Tanto el conocimiento sobre la escena como el problema a resolver y cualquier otro conocimiento debería ser usado para fijar el umbral. La información de la que se puede disponer puede venir proporcionada por las características de los objetos, el tamaño de los mismos, la fracción de la imagen ocupada por los objetos y los diferentes tipos de objetos que pueden parecer en la imagen
Umbralización por el método de Otsu
Se basa en el histograma de la imagen en escala de grises. Después de calcular el histograma se puede inferir algunos parámetros estadísticos. Primero se calcula la media y la varianza globales de los niveles de gris.

Donde l son los niveles de intensidad (valores de 0 a 255) y p(l) es la densidad de probabilidad discreta:

Donde l son los niveles de intensidad (valores de 0 a 255) y p(l) es la densidad de probabilidad discreta:

Donde n es el número de píxeles de la imagen y q n es el número de pixeles que tienen un nivel de intensidad l.
Se supone un umbral U. Se calcula la media y varianza “por debajo” y “por encima” de
U (lo que supone aplicar el concepto de probabilidad condicional a los casos 1<U y 1>U).

Se define la “varianza conjunta después de aplicar el umbral U”:
La diferencia  es una media de la calidad del umbral U. En un caso ideal, donde la imagen tuviera sólo dos niveles de gris se cumpliría 0 = D cuando U no está entre los niveles y 0 2 > = σ D si está entre ellos.
es una media de la calidad del umbral U. En un caso ideal, donde la imagen tuviera sólo dos niveles de gris se cumpliría 0 = D cuando U no está entre los niveles y 0 2 > = σ D si está entre ellos.
El algoritmo cosiste simplemente en calcular D para todos los posibles umbrales y usar el que produce el máximo. Se puede ver que las fórmulas son adecuadas para un cálculo iterativo y rápido (se puede calcular las sumas para un valor de umbral a partir de las anteriores: sumando o restando un valor).
Este método es el más robusto ante cualquier tipo de histograma y de hecho es el más referenciado y utilizado de la literatura.
 es una media de la calidad del umbral U. En un caso ideal, donde la imagen tuviera sólo dos niveles de gris se cumpliría 0 = D cuando U no está entre los niveles y 0 2 > = σ D si está entre ellos.
es una media de la calidad del umbral U. En un caso ideal, donde la imagen tuviera sólo dos niveles de gris se cumpliría 0 = D cuando U no está entre los niveles y 0 2 > = σ D si está entre ellos.El algoritmo cosiste simplemente en calcular D para todos los posibles umbrales y usar el que produce el máximo. Se puede ver que las fórmulas son adecuadas para un cálculo iterativo y rápido (se puede calcular las sumas para un valor de umbral a partir de las anteriores: sumando o restando un valor).
Este método es el más robusto ante cualquier tipo de histograma y de hecho es el más referenciado y utilizado de la literatura.
TRANSFORMADA DE HOUGH
La formulación inicial de esta transformada se realizó sobre el espacio (m, c), también denominado espacio de parámetros, que corresponde a la pendiente y el desplazamiento de la recta.
La formulación inicial de esta transformada se realizó sobre el espacio (m, c), también denominado espacio de parámetros, que corresponde a la pendiente y el desplazamiento de la recta.

Entonces, la idea principal de la trasformada de Hough es:
Recorrer todos los puntos de frontera (bordes), y para cada uno de ellos, acumular un voto en aquellas posiciones del espacio de parámetros que correspondan a una línea que pasa por dicho punto frontera
El objetivo será realizar una transformación de las evidencias del espacio de la imagen
(espacio x-y) al espacio de rectas (espacio m-c). Un solo punto en el espacio m-c corresponde, a una recta en el espacio x-y, por otro lado un punto en el espacio x-y se puede definir como el punto donde cortan las infinitas líneas (para todos los valores de
m) que pasan a través de él. Para un punto (y o, x o), las rectas que pasan a través de él son las rectas que cumplen , es decir, los puntos (m, c) que corresponden a la recta
es decir, los puntos (m, c) que corresponden a la recta del espacio m-c.
del espacio m-c.
Si se considera un conjunto de n puntos alineados ΡI, sólo existe una recta
que pasa a través de todos ellos. Por lo tanto, al dibujar las n rectas del espacio m-c que corresponden a cada uno de los puntos se tiene que todas ellas tienen en común el punto (c o ,m o)
Recorrer todos los puntos de frontera (bordes), y para cada uno de ellos, acumular un voto en aquellas posiciones del espacio de parámetros que correspondan a una línea que pasa por dicho punto frontera
El objetivo será realizar una transformación de las evidencias del espacio de la imagen
(espacio x-y) al espacio de rectas (espacio m-c). Un solo punto en el espacio m-c corresponde, a una recta en el espacio x-y, por otro lado un punto en el espacio x-y se puede definir como el punto donde cortan las infinitas líneas (para todos los valores de
m) que pasan a través de él. Para un punto (y o, x o), las rectas que pasan a través de él son las rectas que cumplen ,
 es decir, los puntos (m, c) que corresponden a la recta
es decir, los puntos (m, c) que corresponden a la recta del espacio m-c.
del espacio m-c.Si se considera un conjunto de n puntos alineados ΡI, sólo existe una recta

que pasa a través de todos ellos. Por lo tanto, al dibujar las n rectas del espacio m-c que corresponden a cada uno de los puntos se tiene que todas ellas tienen en común el punto (c o ,m o)
En la figura se puede ver que las líneas que pasan por un punto del espacio x-y corresponde a una línea en el espacio m-c, figura (b). De igual forma, los puntos alineados del espacio x-y, corresponden a líneas que se cortan en un punto común, es decir, los puntos en una misma línea  corresponden a líneas en el espacio m-c sobre el punto (m o , c o) .
corresponden a líneas en el espacio m-c sobre el punto (m o , c o) .
 corresponden a líneas en el espacio m-c sobre el punto (m o , c o) .
corresponden a líneas en el espacio m-c sobre el punto (m o , c o) . Por lo tanto un método para detectar líneas a partir de un conjunto de puntos ΡI, es interpretar el espacio m-c como un espacio de votación y para cada punto acumular un valor entero correspondiente al número de votos que indican la presencia de esa recta en la imagen. Para calcular el número de votos en cada posición, se hace que para cada punto de I Ρ se incremente en uno todos los puntos que corresponden a la recta del espacio m-c.
Como resultado de lo anterior, en cada punto (m, c) obtenemos un número de votos igual al número de puntos situados sobre la recta y= mx + c . Es decir, la búsqueda de un conjunto de puntos alineados en el espacio x-y se convierte en la búsqueda de un punto con un alto valor de acumulación en el espacio m-c
El atractivo de la transformada de Hough surge de la subdivisión del espacio parámetro en las denominadas celdas acumuladoras, donde son los rangos esperados de los valores de la pendiente y la ordenada.
son los rangos esperados de los valores de la pendiente y la ordenada.
Como resultado de lo anterior, en cada punto (m, c) obtenemos un número de votos igual al número de puntos situados sobre la recta y= mx + c . Es decir, la búsqueda de un conjunto de puntos alineados en el espacio x-y se convierte en la búsqueda de un punto con un alto valor de acumulación en el espacio m-c
El atractivo de la transformada de Hough surge de la subdivisión del espacio parámetro en las denominadas celdas acumuladoras, donde
 son los rangos esperados de los valores de la pendiente y la ordenada.
son los rangos esperados de los valores de la pendiente y la ordenada. 
La celdas de coordenadas (i, j), con valor de acumulador A(i, j), corresponde al cuadrado asociado con el espacio de parámetro (co , mo).
Un problema que aparece al utilizar la ecuación y = mx + c para representar una línea, es que tanto la pendiente como la ordenada en el origen tienden a infinito cuando la línea se acerca a la vertical, una forma de evitar esta dificultad es utilizar la representación normal de la recta, definida sobre los parámetros (ρ , θ).
Un problema que aparece al utilizar la ecuación y = mx + c para representar una línea, es que tanto la pendiente como la ordenada en el origen tienden a infinito cuando la línea se acerca a la vertical, una forma de evitar esta dificultad es utilizar la representación normal de la recta, definida sobre los parámetros (ρ , θ).
ρ = xcosθ + ysenθ
Se puede observar la interpretación de los parámetros de la recta y la subdivisión del espacio de parámetro, donde ρ es la distancia del origen a la recta y θ es el ángulo formado por la recta que une el origen con el punto más cercano y el eje de las abscisas.

El empleo de esta representación en la construcción de una tabla de acumuladores es idéntico al método expuesto para la representación punto – pendiente. Sin embargo, en vez de líneas rectas, los lugares geométricos son curvas sinusoidales en el plano(ρ , θ).
Una vez se haya aplicado la transformada de Hough, se verifica los puntos que tienen valores más altos (picos), estos contienen las líneas de mayor longitud, en la figura se puede observar que se obtiene una gran cantidad de líneas que cruzan toda la imagen, también se puede notar que hay muchas líneas juntas donde solo debería haber una que represente a la línea de borde de la imagen, esto se da porque las líneas que se obtuvieron con la detección de bordes no son completamente rectas o son de mas de un píxel.

Con la obtención de los picos, figura se pasa a eliminar las celdas en la tabla de acumuladores que estén junto a los puntos más altos (para eliminar las líneas que están muy cerca de unas a otras). Con los picos que posiblemente conforman líneas se pasa a verificar si verdaderamente es una línea o es la acumulación de puntos aislados, también se debe encontrar dónde inicia y dónde termina cada línea, y finalmente se agrupan en segmentos de líneas los puntos encontrados, uniendo las discontinuidades en las líneas y suprimiendo los puntos que están aislados obteniendo únicamente las líneas más largas.
ANALISIS DE COMPONENTES CONECTADOS
El etiquetado de componentes conectados, es un método que marca o enumera cada objeto (caracter o caracteres unidos) de una imagen binaria. La figura muestra una imagen con tres objetos, donde, una vez aplicado el algoritmo de componentes conectados los píxeles de la A tendrán un valor de 1, la B de 2 y la C de 3.

Un píxel p de coordenadas (x, y) tiene dos vecinos horizontales y dos verticales, cuyas coordenadas son (x+1, y), (x-1, y), (x, y+1) y (x, y-1), este conjunto de 4 vecinos de p denotados por N4(p), figura 4.5 (a). Los 4 vecinos diagonales de p tienen coordenadas (x+1, y+1),
(x-1, y-1), (x-1, y+1) y (x-1, y-1) denotados por ND(p), figura (b). La unión de N4(p) y ND(p), figura (c), son los 8 vecinos de p denotados por N8(p)
(x-1, y-1), (x-1, y+1) y (x-1, y-1) denotados por ND(p), figura (b). La unión de N4(p) y ND(p), figura (c), son los 8 vecinos de p denotados por N8(p)

Dos píxeles p y q son 4-adyacentes si ) ( 4 p N q ∈ , similarmente p y q son 8-adyacentes si ) ( 8 p N q ∈ , figura (d) y (c) ilustran estos conceptos . Un camino entre los píxeles p1 y pn es una secuencia de píxeles p1, p2,…, pn-1, pn tal que pk es adyacente a pk+1, para n k < ≤ 1 . Un camino puede ser de conectividad 4 o conectividad 8, dependiendo de la definición de adyacencia usada. Dos píxeles p y q de un objeto son de conectividad 4, si existe un camino de conectividad 4 entre ellos, y hay conectividad 8 si existe un camino de conectividad 8 entre ellos, el conjunto de todos los píxeles conectados de un objeto es llamado componente conectado.
ZONIFICACIÓN
Se realiza una división de la imagen en zonas [12], a cada zona se le encuentra el promedio para obtener un único valor, en la figura 5.11 (a) se muestra una imagen de 60 x 25 y el resultado de la zonificación, figura (b) una imagen de 12 x 5.

Donde el vector de características es el valor de cada píxel obtenidos de la zonificación.
VECINO MÁS CERCANO HOLOGRÁFICO
El algoritmo del vecino más cercano holográfico (VMCH) está basado en los principios de Memoria Asociativa Holográfica (MAH) . La MAH basa su concepto en la holografía óptica sobreponiendo múltiples asociaciones de estímulo-respuesta en una misma unidad de procesamiento. Todo esto en el dominio de los números complejos. El vector de datos externos es representado por el conjunto de estímulos-respuestas Donde i s son valores escalares definidos en el conjunto de estímulos-respuestas
S = (s1, 12, ... sM)
y M es el número de variables de entrada. Cada variable de entrada es mapeada a variables polares por el término de relación sigmoidal:
Donde µ es la media y σla desviación estándar para cada variable. La anterior ecuación mapea cada i s a valores de fase entre cero y π 2 El algoritmo VMCH se calcula como la menor distancia euclidiana de las i θ, en donde cada una se obtiene utilizando la siguiente expresión:
Los anteriores parámetros son los vectores de características que han sido mapeados a variables polares por el término de relación sigmoidal. Para identificar cual es el vector de características que representa al caracter, se calcula la distancia euclidiana entre todos los exp i θ de entrenamiento y el nuevo parámetro de entrada, el menor valor de este cálculo será el vector de características o caracter.












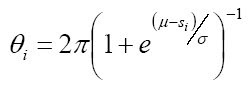

No hay comentarios:
Publicar un comentario